|
|
|
|
|
Uncorrected records |
|
|
Corrected records |
|
|
Elastic response spectra |
After recovering the paper or film from the instrument, the trace of the strong ground motion is digitised either by hand or by machine. This digitised record is then ready for use, after checking that there are no obvious digitisation errors.
The majority of records within this databank were recorded by analogue instruments such as the SMA-1 made by Kinemetrics Inc.
Recently digital instruments have become increasingly deployed but there still fewer digital records in the databank than those from analogue accelerographs. Click here for a list of instrument manufacturers.
Records from analogue instruments are particularly affected by long period errors because of the digitisation stage which is not required for records from digital instruments. An excellent discussion of the errors in digitised analogue records is provided by Trifunac et al. (1973).
|
|
Transducer distortions of amplitude and phase |
|
|
Imperfections of the transducer design: most existing transducers are not true single-degree-of-freedom (SDOF) systems |
|
|
Transverse play of the recording paper/film causing variations up to several millimetres |
|
|
Non-uniform velocity of the record-driving mechanism |
|
|
Non-uniform time marks |
|
|
Misalignment of the transducers |
|
|
Clipping: if sensitivity setting of instrument is too high, the largest peaks may go off scale |
|
|
Variable trace thickness: influences accuracy of digitisation |
|
|
Sensitivity calibration |
|
|
Drift: over long time intervals, temperature and humidity effects can cause drift but for periods of minutes this is not important |
|
|
Instrument slip |
|
|
Warping of film negatives caused by chemical processing and ageing |
|
|
Errors from optical enlargement during printing of film negatives resulting from lens imperfection and non-parallelism of the planes of original film and projected image |
|
|
Poisson effect in film processing because during film copying, the original and copy are held together under longitudinal tension |
|
|
Digitisation rate: the greater the number of digitised points, the better the accuracy with which the digital data approximates the continuous function of the accelerogram | ||||||
|
|
Inadequate resolution of the digitising equipment | ||||||
|
|
Low-pass filtering effects of optical-mechanical digitisation because digitisation approximates a continuous function by a sequence of discrete points | ||||||
|
|
Systematic and random digitisation errors:
|
where ![]() is the undamped
critical damping ratio (usually about 0.6 in most analogue instruments),
is the undamped
critical damping ratio (usually about 0.6 in most analogue instruments), ![]() is the transducer natural angular frequency (usually about 25 × 2
is the transducer natural angular frequency (usually about 25 × 2![]() in most
analogue instruments), Ü ; is the ground acceleration (the dots signify differentiation with respect to time).
in most
analogue instruments), Ü ; is the ground acceleration (the dots signify differentiation with respect to time).
The transducer undamped natural angular frequency, ![]() , is usually high enough so that
y(t) is proportional to the ground acceleration, Ü ;, for frequencies less than about 25Hz. However for higher frequencies it is important
that an instrument correction is performed to find the "true" ground acceleration, Ü ;. A number of different methods have been used to achieve
such a correction, for example a finite difference method (Trifunac, 1972),
high-frequency oscillator approach (Trifunac, 1972), discrete Fourier transform filter
and digital differentiation (Sunder & Connor, 1982).
, is usually high enough so that
y(t) is proportional to the ground acceleration, Ü ;, for frequencies less than about 25Hz. However for higher frequencies it is important
that an instrument correction is performed to find the "true" ground acceleration, Ü ;. A number of different methods have been used to achieve
such a correction, for example a finite difference method (Trifunac, 1972),
high-frequency oscillator approach (Trifunac, 1972), discrete Fourier transform filter
and digital differentiation (Sunder & Connor, 1982).
One of the main polynomial correction methods was developed at the Earthquake Engineering Research Laboratory (California Institute of Technology). A parabolic acceleration baseline (cubic baseline on the velocity) is assumed which is fixed by minimizing the mean square ground velocity (Hudson et al., 1969). Graizer (1979) develops a technique based on this idea and uses this method to correct the 65° component of the Parkfield-Cholame Shandon Array 2W record from the Parkfield earthquake (28/6/1966) and achieves a good match with theoretical results. Graizer (1979) minimizes the mean square ground velocity in the 'quiet' periods before and after the main portion of shaking and also uses polynomials of up to degree 10, thereby achieving a more stable correction.
Iwan et al., 1985 introduce a simple baseline correction method, specifically for the Kinemetrics PDR-1 digital accelerograph, which allows three parts of the acceleration baseline (that before the strong motion, that during the strong motion and that after the strong motion) to have different zero levels. This procedure was used because tests revealed an instrument anomaly, thought to be due to mechanical or electrical hysteresis within the transducer, which prevented the true ground displacement being recovered simply through integrating twice the acceleration time-history. Results obtain by Iwan et al., 1985 for test recordings and for one record from an aftershock of the Coalinga earthquake (8/5/1983, ML=5.5), by Anderson et al., 1986 and Mendez & Anderson, 1991 for records of the Michoacan earthquake (19/9/1985, Mw=8.0), by Boore, 2001 for records from the Chi-Chi earthquake (20/9/1999, Mw=7.6) and by Boore et al., 2001 for records from the Hector Mine earthquake (16/10/1999, Mw=7.1) show that realistic ground displacements can be obtained by this method.
Some of the records in the databank have been individually corrected by the owners of the data and these are included rather than the uniformly processed records. In the header of each file it is clearly stated which processing procedure has been adopted.
Since the short and long period errors present in each record are unique for each type of instrument and digitisation procedure, and because of the random nature of the errors, each accelerogram should ideally be corrected individually. For the normal period range of engineering interest (about 0.1 to 2s) the corrected records catalogued in this databank should be adequate but for periods outside this range caution is advised in the use of the corrected records. The uncorrected records are also included on this website for user who wish to apply their own correction methods. Some records were only provided by the data owners in already corrected format.
|
|
maximum absolute response acceleration Sa =max t |ü +Ü |, |
|
|
maximum relative response velocity Sv =max t | |
|
|
maximum relative response displacement Sd =max t | u |. |
Two external forces act on the mass one is due to the spring and the other due to the equivalent viscous damping. These forces must resist the total inertial forces of the system, m ü and m Ü hence, m Sa gives the maximum base shear force acting which must be resisted by the system.
From the relative response displacement two 'pseudo' values can be calculated:
|
|
maximum absolute pseudo-acceleration S'a =(2 |
|
|
maximum relative pseudo-velocity S'v =(2 |
m S'a gives the force which must be resisted by the spring (Chopra, 1995) and not the complete system. For small coefficients of critical damping and relatively short periods Sa and S'a are almost identical (Chopra, 1995).
Maximum relative pseudo-velocity, S'v , is related to the peak value of strain energy, ES , stored in the system during the earthquake by the equation: ES =m Sv'2/2 (Chopra, 1995, p. 200).
A plot of the quantities defined above as a function of the natural vibration period, T, and the critical damping ratio,
![]() , of the system is called a response spectrum.
It provides a convenient means of summarizing the peak response of all possible linear SDOF systems to a
particular component of ground motion (Chopra, 1995).
, of the system is called a response spectrum.
It provides a convenient means of summarizing the peak response of all possible linear SDOF systems to a
particular component of ground motion (Chopra, 1995).
The concept and usefulness of response spectra for earthquake engineering is laid out in Benioff (1934) although no spectra are calculated. He states 'suppose we substitute for the engineering structures a series of undamped pendulum seismometers having frequencies ranging from the lowest fundamental frequency of engineering structures to the highest significant overtones. During an earthquake each component seismometer would write a characteristic seismogram. Plotting the maximum recorded deflection of each pendulum against its frequency, we obtain a curve which may be termed the undamped pendular spectrum of the earthquake.'
Consider the SDOF system illustrated in Figure 1. This system consists of a mass m, moving on a frictionless surface, driven by a horizontal ground motion with acceleration Ü , with a spring with stiffness k and a dashpot with a coefficient of viscous damping c .
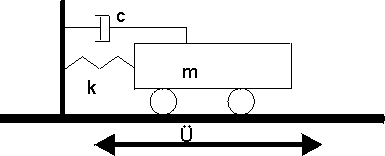
Figure 1
Let u(t) be the horizontal displacement of the mass at time t . Then using Newton's second law and resolving forces horizontally gives:
Dividing by m and defining
![]() 0=
0= ![]() and
and
![]() 0=c/2
0=c/2
![]() 0m as the critical damping ratio yields:
0m as the critical damping ratio yields:
|
| (1) |
Equation 1 is essential for modelling the linear response of structures to earthquake excitation, see for example Chopra (1995).
Equation 1 is the simplest second order differential equations possible and because it models many oscillatory phenomena it has been much studied even before strong-motion records of earthquakes were obtained.
In 1933 the first accelerograms were written during the Long Beach earthquake (11/3/1933) and so the calculation of response spectra became possible.
Benioff (1934) used Equation 1, with
![]() 0=0, to construct six (one for each horizontal
component) undamped response spectra for three western North American strong-motion records. He mentions that
undamped and linear elastic models do not really reflect a buildings behaviour implying some damping, i.e.
0=0, to construct six (one for each horizontal
component) undamped response spectra for three western North American strong-motion records. He mentions that
undamped and linear elastic models do not really reflect a buildings behaviour implying some damping, i.e.
![]() 0
0![]() 0,
and inelastic behaviour, are required for more realistic results. He mentions that the calculation of one
response spectrum took 8 hours and cost $40, this compares with today when a single spectrum takes less
than a second to compute and is practically free.
0,
and inelastic behaviour, are required for more realistic results. He mentions that the calculation of one
response spectrum took 8 hours and cost $40, this compares with today when a single spectrum takes less
than a second to compute and is practically free.
Much of the early work on response spectra computed from strong-motion records, using Equation 1, was done by Housner and his co-workers in the 1940s and early 1950s, for example Housner (1941). Damped response spectra were calculated by Alford et al. (1951) and published by Housner et al. (1953). Again the inelasticity of structures for large strains is noted.
After the 1950s response spectra became well established as one of the major tools for assessing strong motion and its effect on structures. Almost all compilations of strong-motion observations from earthquakes include response spectra. For example Brady et al. (1973) shows response quantities at damping and natural period intervals commonly in use today. Since the advent of faster computers Sa , Sv and Sd are often calculated as well as the pseudo quantities, S'a and S'v .
In this project elastic response spectra have been calculated by the efficient algorithm of Nigam & Jennings (1969) and presented in a standard format for spectral data. Spectra have been determined from the corrected records only. The period range is between 0.04s and 4.0s. Spectra have been calculated at 5 critcal damping ratios of 0, 2, 5, 10 and 20%. Absolute acceleration, Sa , relative-velocity, Sv , relative-displacement, Sd , and pseudo-velocity spectra, S' v , are presented.
|
|